Exploring Median Control Charts
Median control charts: A viable alternative to individual charts
Median control charts, also known as x̃ control charts, fill a crucial gap between individual charts and averages charts (Xbar charts). While averages charts, paired with either range charts or sigma charts, are the preferred statistical process control (SPC) tool for variables data, there are circumstances when Xbar charts aren’t practical. These instances open the door for the use of median control charts.
The strengths of Xbar charts lie in the normalizing influence of the central limit theorem, customizable sensitivity via subgroup size adjustment, optimized estimation of process variation through rational subgrouping, graphical control of dispersion, and the independence of data points on the Xbar chart, which facilitates run testing. When Xbar charts aren’t applicable, individual charts paired with moving range charts become the default choice.
However, there are instances when Xbar charts aren’t applicable, like when the workforce lacks the training needed for the calculations involved. Under such conditions, despite the theoretical feasibility and lack of economic or scientific reasons against the use of Xbar charts, median control charts might serve as a more suitable alternative to individual charts. The sensitivity of median charts, like Xbar charts, can be adjusted by manipulating the subgroup size.
Here are steps to effectively use median control charts:
- Establish the subgroup size and sampling frequency. Generally, subgroups of three, five, or seven units are used, with groups of five being most common. Odd-sized subgroups are often chosen as they eliminate the need for calculations. The subgroup size impacts the sensitivity of the control chart. Smaller subgroups result in less sensitive control charts, while larger subgroups might be overly sensitive to small, economically insignificant changes. With median charts, it is advisable to keep the subgroup size small — no more than nine. Median charts are statistically less efficient than Xbar charts, and this inefficiency escalates as the subgroup size increases.
- Aim to gather data from 20-25 subgroups, equating to a minimum of 100 individual values. Minimize disturbances to the process while collecting data. If a process change is inevitable, devise a system for recording changes so their effects can be assessed. Any changes should be noted directly on the chart.
- Compute the control limits using appropriate equations. The choice of the Ã2 constant depends on your subgroup size, n.
| n | Ã2 | D4 |
|---|---|---|
| 3 | 1.187 | 2.575 |
| 5 | 0.691 | 2.115 |
| 7 | 0.508 | 1.924 |
| 9 | 0.412 | 1.816 |
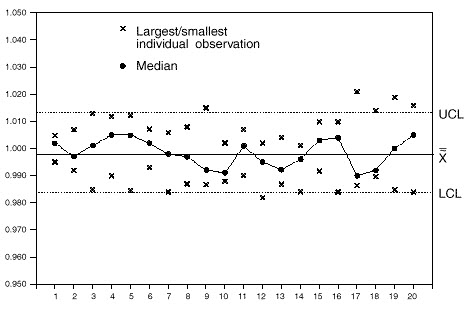
Average\ \tilde{x}=\frac{sum\ of\ medians}{number\ of\ medians}=\bar{\tilde{x}}LCL=\bar{\tilde{x}}-\tilde{A_{2}}\bar{R}UCL=\bar{\tilde{x}}+\tilde{A_{2}}\bar{R}For instance, Table 1 presents the raw data. Each subgroup contains five observations, meaning the subgroup x is simply the middle value. Figure 1 depicts the completed control chart. The smallest and largest points are plotted on the median charts, clearly identifying the median value of each subgroup. A line connects these median values. A range chart should be used during the initial capability study to ascertain if the process dispersion is in control. The average range (Rbar) value from the range chart is also needed to establish the control limits for the median chart.
| Row | No. 1 | No. 2 | No. 3 | No. 4 | No. 5 | x̃ | R |
|---|---|---|---|---|---|---|---|
| 1 | 1.002 | 0.995 | 1.000 | 1.002 | 1.005 | 1.002 | 0.010 |
| 2 | 1.000 | 0.997 | 1.007 | 0.992 | 0.995 | 0.997 | 0.015 |
| 3 | 0.997 | 1.013 | 1.001 | 0.985 | 1.002 | 1.001 | 0.028 |
| 4 | 0.990 | 1.008 | 1.005 | 0.994 | 1.012 | 1.005 | 0.022 |
| 5 | 0.992 | 1.012 | 1.005 | 0.985 | 1.006 | 1.005 | 0.027 |
| 6 | 1.000 | 1.002 | 1.006 | 1.007 | 0.993 | 1.002 | 0.014 |
| 7 | 0.984 | 0.994 | 0.998 | 1.006 | 1.002 | 0.998 | 0.022 |
| 8 | 0.987 | 0.994 | 1.002 | 0.997 | 1.008 | 0.997 | 0.021 |
| 9 | 0.992 | 0.988 | 1.015 | 0.987 | 1.006 | 0.992 | 0.028 |
| 10 | 0.994 | 0.990 | 0.991 | 1.002 | 0.988 | 0.991 | 0.014 |
| 11 | 1.007 | 1.008 | 0.990 | 1.001 | 0.999 | 1.001 | 0.018 |
| 12 | 0.995 | 0.989 | 0.982 | 0.995 | 1.002 | 0.995 | 0.020 |
| 13 | 0.987 | 1.004 | 0.992 | 1.002 | 0.992 | 0.992 | 0.017 |
| 14 | 0.991 | 1.001 | 0.996 | 0.997 | 0.984 | 0.996 | 0.017 |
| 15 | 1.004 | 0.993 | 1.003 | 0.992 | 1.010 | 1.003 | 0.018 |
| 16 | 1.004 | 1.010 | 0.984 | 0.997 | 1.008 | 1.004 | 0.026 |
| 17 | 0.990 | 1.021 | 0.995 | 0.987 | 0.989 | 0.990 | 0.034 |
| 18 | 1.003 | 0.992 | 0.992 | 0.990 | 1.014 | 0.992 | 0.024 |
| 19 | 1.000 | 0.985 | 1.019 | 1.002 | 0.986 | 1.000 | 0.034 |
| 20 | 0.996 | 0.984 | 1.005 | 1.016 | 1.012 | 1.005 | 0.032 |
When employing control charts, keep the following tips in mind:
- Be prompt! Control charts are tools designed to assist in process improvement by identifying special causes. It’s of little value knowing a special cause existed in the past; timely detection is crucial. Otherwise, identifying the special cause becomes impossible, leaving only a “ghost”. Regular small samples are generally more effective than infrequent large ones in capturing these ghosts.
- Record as much background information as possible. This data can be invaluable in analyzing patterns that may otherwise seem random.
- Make notes directly on the chart form. The most valuable control charts often aren’t the cleanest ones; they’re the ones that have been actively used.
- Embrace an active investigator role. Simply using control charts to “study history” only leverages half of their potential benefit. Deliberately trying different things, noting these experiments on the charts, can significantly expedite the learning process.
If a point falls out of control, check the simple things first, such as ensuring the calculations were correct and the point is plotted correctly. A written procedure or flowchart outlining the steps to take when a subgroup median falls beyond a control limit should be in place. This procedure should also cover the steps to be taken if the special cause cannot be identified.