Sam handed Peter a computer printout and asked, “If the yields are so high, why is my efficiency so low?”
Peter, a Lean Six Sigma Black Belt, studied the report for a moment and then nodded. “Let me show you what’s going on,” he said as he picked up a marker and drew a diagram (see Figure 1).
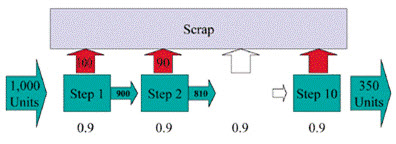
“This process has 10 separate steps,” Peter began. “Each step has a yield of about 90 percent. This is the unit yield for that process step.”
“Right,” Sam interjected. “And all of them are about 90 percent, so the average yield for the whole process should be about 90 percent.”
“Yes, but that isn’t the number you need if you’re trying to determine the final yield for the process,” Peter responded. “Final yield, which is sometimes called the rolled throughput yield (RTY), is the proportion of defect-free units out of the final process step relative to what you started with at the first process step.”
Sam nodded. “Yeah, but even though the average yield is nearly 90 percent, our final yield is nowhere near that high.”
Peter turned back to the board. “Here’s a mathematical model of what happens when all process steps have the same unit yield.” He wrote an equation:
Y_{overall}= (Y_{step})^\text{number of steps}“The unit yield at every step is about 0.9, but you have to multiply the step unit yields together to get the final unit yield. You can’t just average them,” Peter explained. “Think of a simple two-stage process. You start 100 units at the first step and 90 pass. These 90 start the second step and 90 percent of them pass, leaving 81. The average unit yield is 90 percent, but the final unit yield is only 81 percent.”
“So for our 10-step process,” Sam began.
Peter punched his calculator keys. “0.9 raised to the 10th power is about 0.35. So 35 percent is your predicted final yield.”
“And that’s pretty close to what we’re getting,” Sam said.
Peter knew that misunderstandings on yields lead to a variety of poor management decisions. He was pleased that Sam had asked for clarification. But, Peter knew, Sam still didn’t know the whole picture. Six Sigma requires an entirely different mental model of yields.
“That’s not all,” Peter said. “So far we’ve been talking about unit yields. That’s the customary way of doing it around here, but there’s a better way.”
“Unit yields often have very little to do with costs,” Peter continued. “Who knows how we got those 350 good units? Maybe they were reworked several times. There can be a lot of cost hidden in the numbers. If you want an accurate picture of process performance, use rolled throughput yields.”
Peter sketched another picture on the board (see Figure 2).
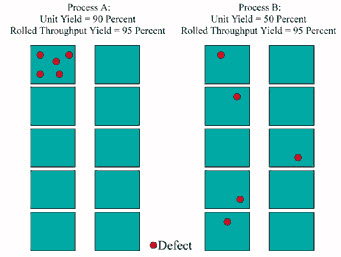
“Let’s assume that we have two lines making the same product. If we only look at unit yields, they look much different. One process has a 50-percent yield, the other a 90-percent yield. But assume that each unit had 10 critical-to-quality characteristics. If we look at characteristics, we see that both have produced five defects in 100 defect opportunities. In terms of the ability to produce defect-free quality characteristics, they’re actually the same.”
“So if it costs $100 to fix a defect, the two processes have about the same rework cost, even though the unit yields would make the first process look a lot better,” Sam replied, nodding.
“This is exactly why we use rolled throughput yields in six sigma,” Peter responded. “They correlate much more closely with labor, cycle time, rework costs and other important management metrics.”
Sam frowned. “That means that our efficiency reports are worse than useless–they’re misleading!”
Peter smiled.
“Thanks, Peter!” Sam exclaimed. “I think you’re just the man to head a project to fix them!”
Yields: A Glossary
Yield, First-time Yield (unit-based): The number of units that pass a particular inspection compared to the total number of units that pass through that point in the process.
Final Yield (unit-based): The number of units that pass the last step in a series of steps in a process compared to the number of units the entire process started with.
Throughput Yield (defect-based): The probability that all defect opportunities produced at a particular step in the process will conform to their respective performance standards.
Rolled Throughput Yield (defect-based): The probability of being able to pass a unit of product or service through the entire process defect-free.
Normalized Yield (defect-based): The geometric average throughput yield one would expect at any given step in the process. Analogous to the “typical” yield. For a k -step process, the normalized yield would be the kth root of the rolled throughput yield. A note of caution: This metric can be misleading if the throughput yields of the process steps vary a great deal.


Leave a Reply